A particle has a de broglie wavelength of 2.7 – A particle with a de Broglie wavelength of 2.7: this intriguing concept opens a window into the fascinating realm of quantum mechanics, where the boundaries between particles and waves blur. This exploration delves into the implications of this wavelength, providing insights into the wave-particle duality of matter and its profound impact on our understanding of the universe.
The de Broglie wavelength, named after physicist Louis de Broglie, is a fundamental property of matter that reveals its wave-like nature. This wavelength is inversely proportional to the particle’s momentum, connecting the microscopic world of particles to the macroscopic realm of waves.
Its discovery has revolutionized our understanding of the fundamental nature of matter and laid the groundwork for quantum mechanics.
De Broglie Wavelength

The de Broglie wavelength is a fundamental concept in quantum mechanics that describes the wave-like properties of matter. It is named after the French physicist Louis de Broglie, who proposed in 1924 that all particles, not just photons, have a wave-like nature.
The de Broglie wavelength is given by the following formula:
λ = h/p
where:
- λ is the de Broglie wavelength
- h is Planck’s constant
- p is the momentum of the particle
The de Broglie wavelength has important implications for the wave-particle duality of matter. It shows that all matter has both wave-like and particle-like properties, and that the wave-like properties become more pronounced as the momentum of the particle decreases.
Applications of de Broglie Wavelength
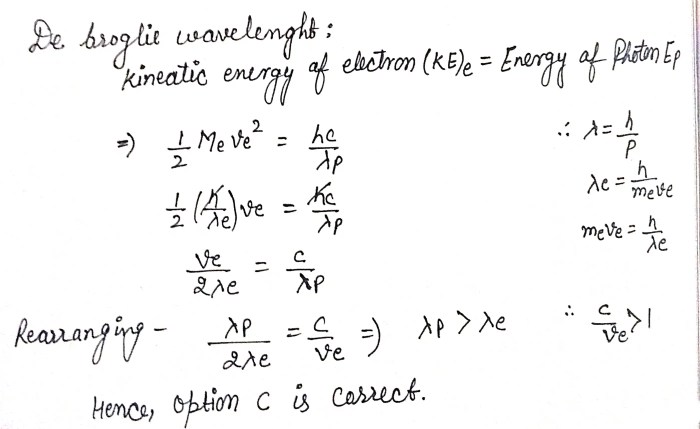
The de Broglie wavelength has a wide range of applications in science and technology, including:
Electron Microscopy
The de Broglie wavelength of electrons is very short, making it possible to use electrons to probe the structure of atoms and molecules. Electron microscopes use a beam of electrons to create images of objects with much higher resolution than optical microscopes.
Development of Quantum Mechanics, A particle has a de broglie wavelength of 2.7
The de Broglie wavelength played a key role in the development of quantum mechanics. It helped to establish the wave-particle duality of matter and led to the development of the Schrödinger equation, which is one of the fundamental equations of quantum mechanics.
Other Potential Applications
The de Broglie wavelength has a number of potential applications, including:
- Atom interferometry
- Quantum computing
- Nanotechnology
Experimental Verification of de Broglie Wavelength

The de Broglie wavelength was experimentally verified by the Davisson-Germer experiment in 1927. In this experiment, a beam of electrons was scattered from a crystal lattice. The scattered electrons were detected on a screen, and the results showed a diffraction pattern that was consistent with the de Broglie wavelength.
The Davisson-Germer experiment was a landmark experiment that confirmed the wave-particle duality of matter and provided strong support for the de Broglie hypothesis.
de Broglie Wavelength and Quantum Mechanics

The de Broglie wavelength is closely related to the wave function in quantum mechanics. The wave function is a mathematical function that describes the state of a particle. The square of the wave function gives the probability of finding the particle at a given location.
The de Broglie wavelength is related to the wave function by the following formula:
λ = h/p = 2πh/mv
where:
- λ is the de Broglie wavelength
- h is Planck’s constant
- p is the momentum of the particle
- m is the mass of the particle
- v is the velocity of the particle
The de Broglie wavelength is a fundamental concept in quantum mechanics. It is used to describe the wave-like properties of matter and to calculate the probability of finding a particle at a given location.
Answers to Common Questions: A Particle Has A De Broglie Wavelength Of 2.7
What is the de Broglie wavelength?
The de Broglie wavelength is a wave-like property associated with particles, inversely proportional to their momentum. It connects the particle’s momentum to its wave-like characteristics.
How is the de Broglie wavelength calculated?
The de Broglie wavelength is calculated using the formula λ = h/p, where λ is the wavelength, h is Planck’s constant, and p is the particle’s momentum.
What is the significance of the de Broglie wavelength?
The de Broglie wavelength highlights the wave-particle duality of matter, demonstrating that particles also possess wave-like properties. This concept is fundamental to quantum mechanics.